"三角形の法則なら1分でディスプレイが完成する" 著書『今あるもので「あか抜けた」部屋になる。』 お部屋づくりののルールを紹介していまして、その中の1つです。 先日出演したnhk 「あさイチ」でもお話しました。 この赤い三角形はスタッフさんの"三角形の法則なら1分でディスプレイが完成する" 著書『今あるもので「あか抜けた」部屋になる。』 お部屋づくりののルールを紹介していまして、その中の1つです。 先日出演したnhk 「あさイチ」でもお話しました。 この赤い三角形はスタッフさんのあなたはどんな法則を知っていますか? 今日は私が大切にしている 人生の三角形の法則について お伝えしていきます! この法則は、さまざな場面で 当てはめることができるので 知っておいて損はしない法則です☆ 人生の三角形の法則とは
七五三 三角形から円に内接する四角形へ
ディスプレイ 三角形 の 法則
ディスプレイ 三角形 の 法則-パスカルの三角形 和の法則 まわり道しないで、左下から右上までいく道順(みちじゅん)は何通り? そう、6通りですね。 では、下の図では何通りかな? 高校生なら、ワンパターンで(?)パッと答えをだすかもしれませんね。(abc) 4 の三角形の12ab 2 cを例に説明します。 (abc) 3 の三角形において、(abc) 4 の三角形の12ab 2 cと同じ位置にあたるのは6abcです。 また、6abcの上に位置するのは3ab 2 、3b 2 cです。 それぞれの項の文字だけをみると、(abc) 3 の三角形のabc,ab 2,b 2 cは(abc) 4 の三角形のab 2 cをそれぞれb,c,aで割った



ヘロンの公式 Wikipedia
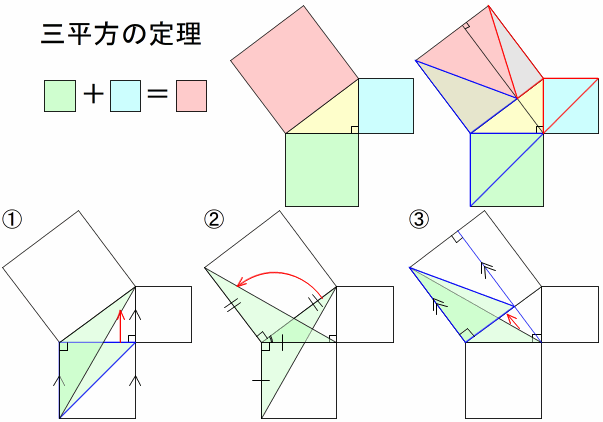
直角三角形の各辺の長さの関係はピタゴラスの定理(三平方の定理)と呼ばれる。 記号⊿を使ってあらわすことがある。 直角三角形の直角以外の2つの角を、直角三角形の鋭角 と呼ぶ。それらの大きさの和は、直角に等しい。パスカルの三角形の使い道 それでは、このパスカルの三角形というものが どういった場面で役に立つのか、それは 展開公式の係数を調べることができる! という点です。 例えば、\((ab)^4\)の展開を考える場合 パスカルの三角形の5段目を見ると三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から)
三角形の外心、三角形の外接円 この1点で交わった点 o を三角形の外心という。 外心 o を中心として、半径 oa の円が三角形 abc の外接円である。 oa=ob=oc ol⊥bc 、 om⊥ac 、 on⊥abこの三角形に並べられた数字には、次のような法則があるのがわかります。 「ある数は、その1つ上の行の隣接する左右の数の和によって求まる」 例えば、上図の赤い部分では、 6+4=10 となっています。ヘロンの公式(ヘロンのこうしき、英 Heron's formula )とは、3辺の長さが a, b, c などと分かっている三角形の面積 S を求める公式のことである。 アレクサンドリアのヘロンが彼の著書『Metrica』の中で証明を与えていることから彼に帰せられる
22 正弦法則 sin Ù sin = sin Ú sin = sin Û sin 23 正接法則 tan Ù− Ú 2 tan Ù Ú 2 = tan − 2 tan 2 tan Ú− Û 2 tan Ú Û 2 tan − 2 tan 2 1 の対象とする球面三角形の幾何学的配 𝜸 球面三角法の簡潔かつ体系的な理解への試み 115数学Aの円で使う定理・性質の一覧 円周角の定理 弧ABに対する円周角の大きさはつねに一定であり、その角の大きさは、その弧に対する中心角の大きさの半分である。 ・∠acb=∠adb ・∠aob=2∠acb=2∠adb また、次の図のよ余弦定理(よげんていり、英 law of cosines, cosine formula )とは、平面上の三角法において三角形の辺の長さと内角の余弦の間に成り立つ関係を与える定理である。 余弦定理を証明するために用いられる補題はときに第一余弦定理と呼ばれ、このとき証明される定理は第二余弦定理と呼ばれ区別さ



三平方の定理 自動計算サイト



数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo
三角形ABCの辺BC,CA,AB上に点D,E,Fをとり、線分AD,BE,CFが1点Gで交わるとき、以下の等式が成り立つ。 チェバの定理の証明 図のように、a= BCG、b= CAG、c= ABG とします。しかも 個以上の三角形を見つけられれば、IQ1以上確実! ということで、この問題は多くのTwitter民たちのクイズ心に火を点けたもよう。ネット上には様々な回答が寄せられている。 あなたはいくつの三角形が隠れているか分かるだろうか?しかも 個以上の三角形を見つけられれば、IQ1以上確実! ということで、この問題は多くのTwitter民たちのクイズ心に火を点けたもよう。ネット上には様々な回答が寄せられている。 あなたはいくつの三角形が隠れているか分かるだろうか?
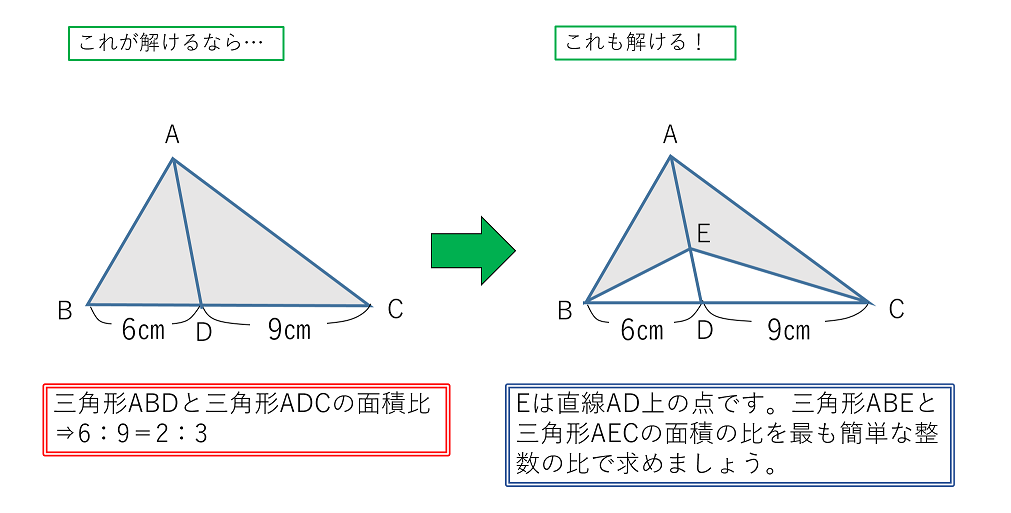


平面図形をマスター 三角形の面積比 応用編その3 中学受験ナビ
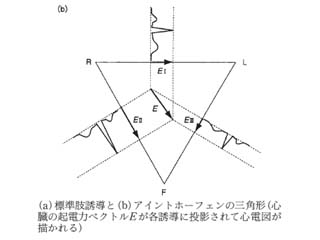


アイントホーフェンの法則とは コトバンク
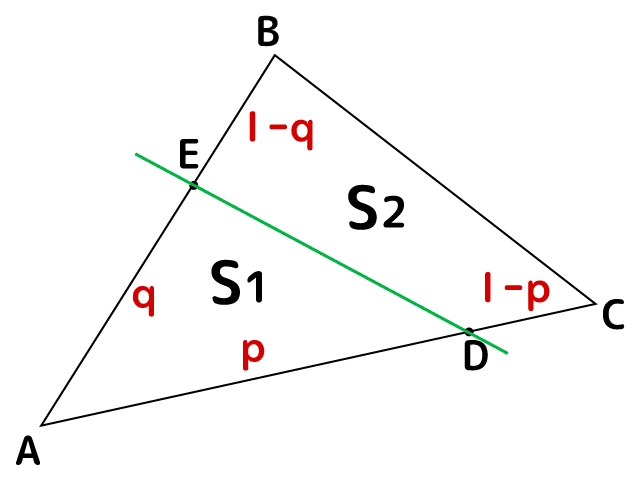
→ 印刷用pdf版は別頁 三角関数の加法定理,倍角公式,3倍角公式,半角公式 三角関数の和や積には多くの公式がありますが,「加法定理は覚える,他は作る」というのが,作者おすすめの考え方です。・・・ただし,そういう公式があるということと,およその形は記憶にとどめます。解説:三角形面積2等分の法則 三角形を2等分する有名な公式があります: 上図のようにADDC=p1p及びAEEB=q1qと内分した時、 であれば緑の直線は三角形の面積を2等分します(この理由は後述で深堀します)。この法則を設問に照らし合わせてみましょう。逆三角形型の文章を書くには 三角形型は物語調ですから,それでどうなるのだろうと思いながら読み進めてもらうにはよい のですが,手っ取り早く何が書いてあるのかを伝えるという点では適しているとは言えません。 それに対し,逆三角形型は何が書い



逆三角形の法則でロジックを絞り込みましょう 地方自治体の宣伝や広報でお悩みの担当者さん 必見 宣伝の新しい形


三平方の定理が一瞬で理解できる 公式 証明から計算問題まで解説 Studyplus スタディプラス
三角形(さんかくけい、さんかっけい、拉 triangulum, 独 Dreieck, 英, 仏 triangle, (古風) trigon) は、同一直線上にない3点と、それらを結ぶ3つの線分からなる多角形。 その3点を三角形の頂点、3つの線分を三角形の辺という。三角形の面積(1辺と2角から) 正方形の面積 長方形の面積 台形の面積 台形の高さ・面積(4辺の長さから) 台形の1辺・面積(3辺の長さと高さから) ひし形の面積 平行四辺形の面積(底辺と高さから) 平行四辺形の面積(2辺と夾角から)逆三角形の法則 そう、お客さんにプレゼンするには この順番、法則がすごく大事です。 今日の話は、会社のコンセプトを 決めるのと同じくらい 重要な内容ですので、 ぜひ時間を作って考えてみてくださいね。 それでは今日は この辺で失礼致します。



中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
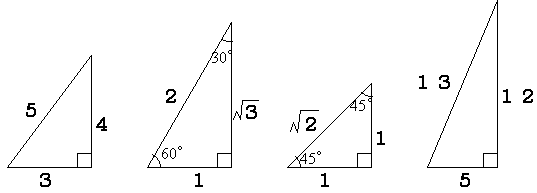


三角形の性質
パスカルの三角形(パスカルのさんかくけい、英 Pascal's triangle )は、二項展開における係数を三角形状に並べたものである。 ブレーズ・パスカル(1623年 1662年)の名前がついているが、実際にはパスカルより何世紀も前の数学者たちも研究していた。 この三角形の作り方は単純なルールに逆三角形型の文章を書くには 三角形型は物語調ですから,それでどうなるのだろうと思いながら読み進めてもらうにはよい のですが,手っ取り早く何が書いてあるのかを伝えるという点では適しているとは言えません。 それに対し,逆三角形型は何が書い22 正弦法則 sin Ù sin = sin Ú sin = sin Û sin 23 正接法則 tan Ù− Ú 2 tan Ù Ú 2 = tan − 2 tan 2 tan Ú− Û 2 tan Ú Û 2 tan − 2 tan 2 1 の対象とする球面三角形の幾何学的配 𝜸 球面三角法の簡潔かつ体系的な理解への試み 115



チェバの定理 Wikipedia



鏡の法則の本質的な意味 鏡の法則は実は三角形だった 一家に一人のセラピストー戦場で働く男性を癒すパートナーシップ論ー ライフシフト総合研究所
三角形の合同条件と相似条件を一気に覚えたい! こんにちは!この記事を書いてる Kenだよ。分子を振動させたね。 中2と中3数学の平面図形で、 三角形の「合同条件」と「相似条件」 を勉強してきたよね。三角形の3つの角の二等分線は1点で交わる 定理8 abcの∠bと∠cの二等分線の交点をdとすると線分adは ∠aを2等分することを証明する。 定理8の証明 点dより各辺に垂線をおろし図↓のようにp,q,rとする三角形は三辺ありますがその三辺の比率をを3:4:5にすると 直角三角形になります。 式にすると √3+√4=√5 です。 これはすごく便利な法則ですので ぜひ覚えたほうがいいです。 diyでもよく使います。 特に外での作業で使うことが多いです。



余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ



中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su
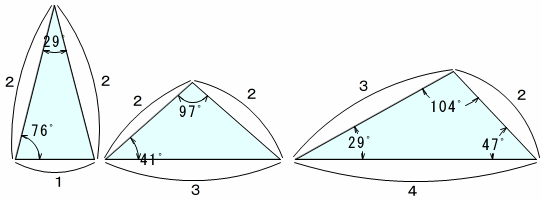
法則はないか s:三角形の形に何か法則があるのかな。三角形の数は幅によって違う。 s:幅が大きくなると、三角形の数は少なくなるし、三角形は大きくなる。 s:同じ紙の三角形は合同なようだけど、違う紙のと比べると合同でもないし、相似でもない。初等幾何学におけるピタゴラスの定理(ピタゴラスのていり、英 Pythagorean theorem )は、直角三角形の3辺の長さの関係を表す。 斜辺の長さを c, 他の2辺の長さを a, b とすると、定理は = が成り立つという等式の形で述べられる 。 三平方の定理(さんへいほうのていり)、勾股弦の定理(こう三角形は三辺ありますがその三辺の比率をを3:4:5にすると 直角三角形になります。 式にすると √3+√4=√5 です。 これはすごく便利な法則ですので ぜひ覚えたほうがいいです。 diyでもよく使います。 特に外での作業で使うことが多いです。



三平方の定理 特別な直角三角形の3辺の比 中学生からの質問 数学 進研ゼミ中学講座 ベネッセコーポレーション



ピタゴラスの定理 Wikipedia
三角形ABCの辺BC,CA,AB上に点D,E,Fをとり、線分AD,BE,CFが1点Gで交わるとき、以下の等式が成り立つ。 チェバの定理の証明 図のように、a= BCG、b= CAG、c= ABG とします。



5分で分かる 正弦定理の公式と覚え方 解き方とは 練習問題でマスターしよう 高校生向け受験応援メディア 受験のミカタ



中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット



中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su



中3数学 3 4 5の直角三角形の辺の長さを求める3つの問題 Qikeru 学びを楽しくわかりやすく
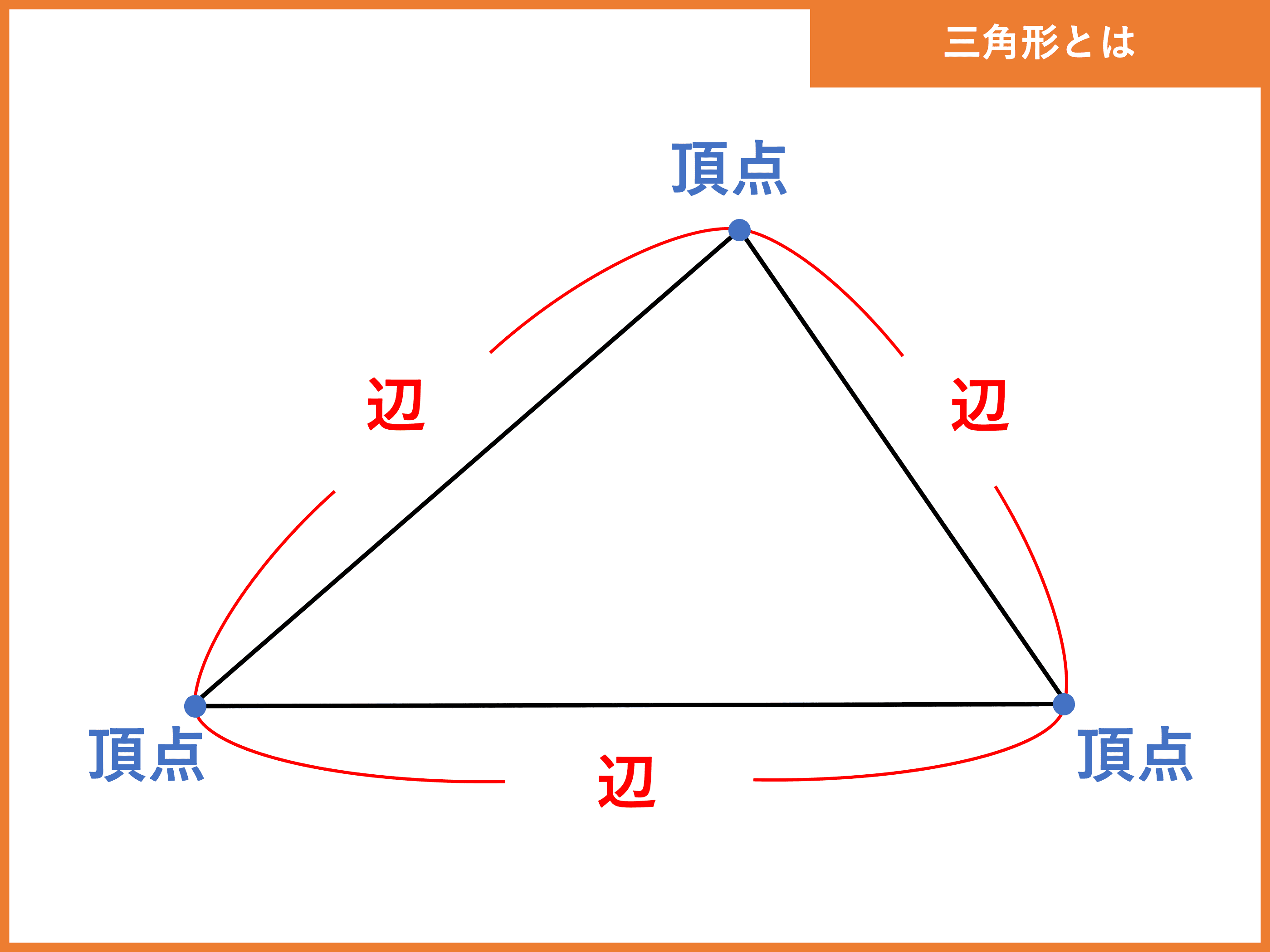


三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
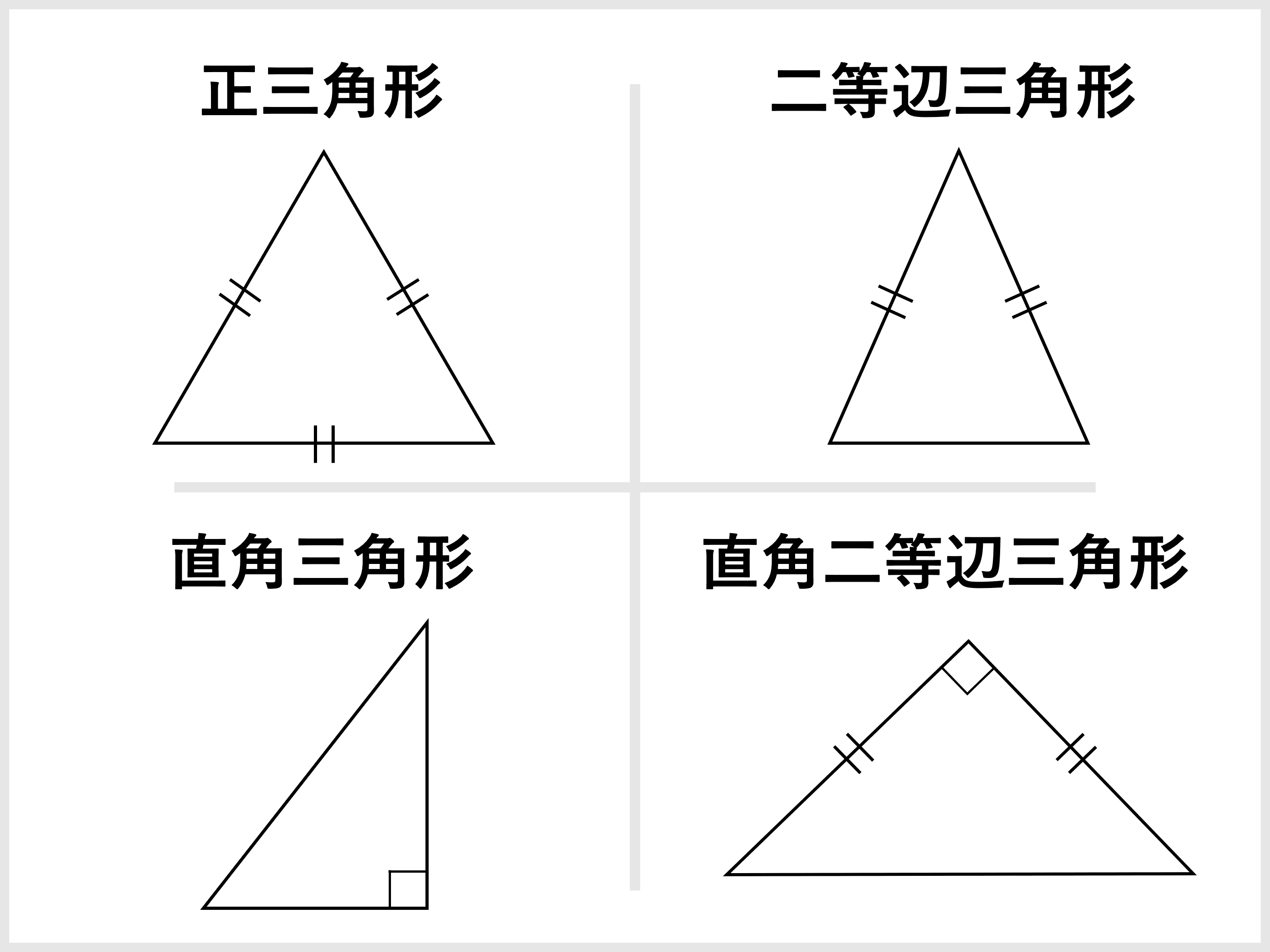


三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典
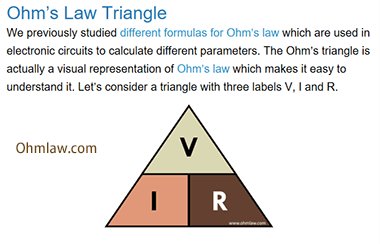


Kistenkasten723 A Twitter オームの三角形 日本では オームの法則の図は 円で描かれるが 英語圏やドイツ語圏では 三角形で表現され Ohm S Law Triangle と呼ばれる 掛算 超算数 算数 算数教育 オームの法則 みはじ図 くもわ図 きはじ T Co


三平方の定理


パスカルの三角形と最短経路 思考力を鍛える数学
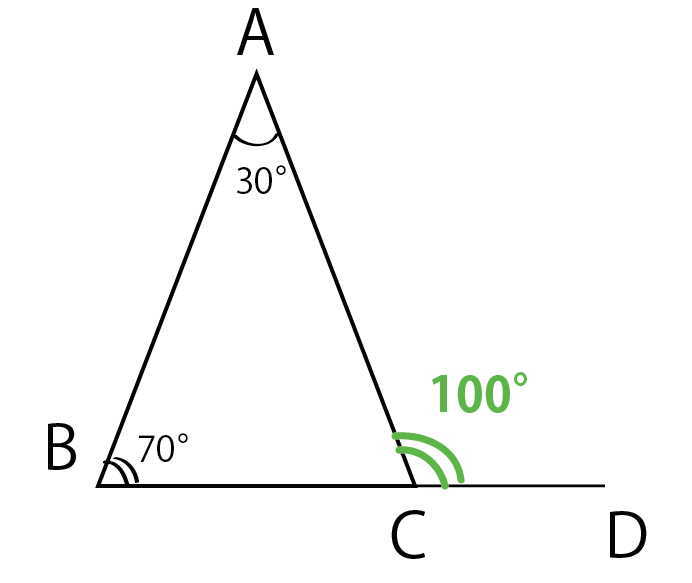


3分でわかる 三角形の外角の定理の証明 Qikeru 学びを楽しくわかりやすく



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に



直角三角形の辺の長さ 合同条件 面積について アタリマエ



数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三平方の定理 直角三角形の辺の長さを計算する4つの問題の解き方 Qikeru 学びを楽しくわかりやすく


パスカルの三角形と最短経路 思考力を鍛える数学
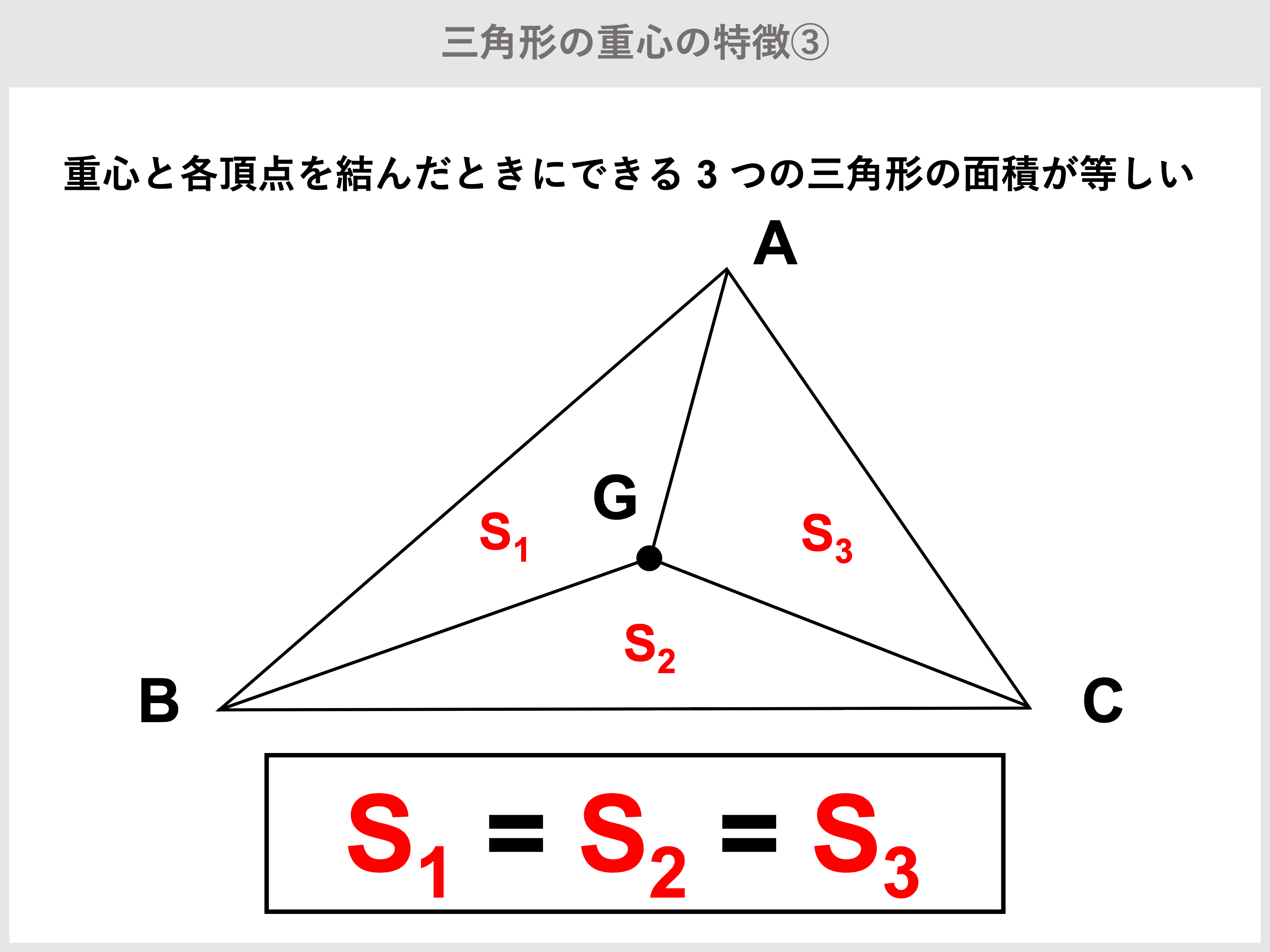


三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典



ヘロンの公式で三角形の面積を求める 三辺の長さがわかっているときはコレ 数学の面白いこと 役に立つことをまとめたサイト



三平方の定理を使って面積を求める 無料で使える中学学習プリント



ヘロンの公式とは 図解でわかるその仕組みと証明方法 アタリマエ
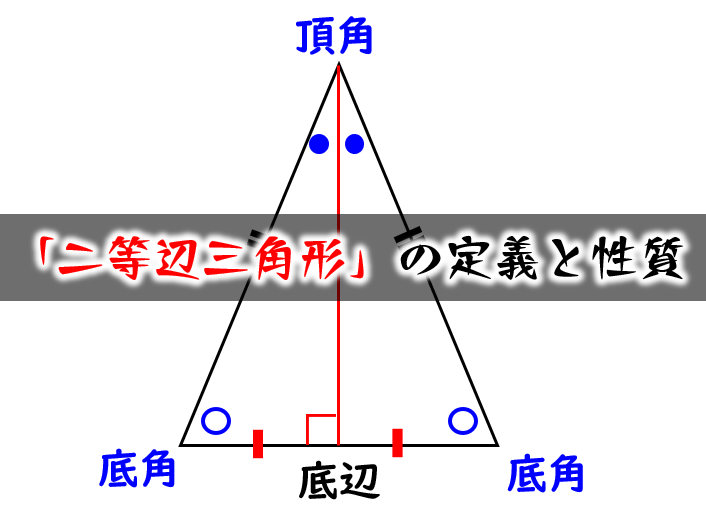


二等辺三角形の定義と性質 問題の解き方 数学fun



中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット


3 4 5の三角形で 本当に直角ができる Note Board



3分でわかる 三平方の定理 ピタゴラスの定理 の公式とは Qikeru 学びを楽しくわかりやすく



三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



三平方の定理 無料で使える中学学習プリント



接弦定理とは何か 角度別に分かるその証明方法 アタリマエ
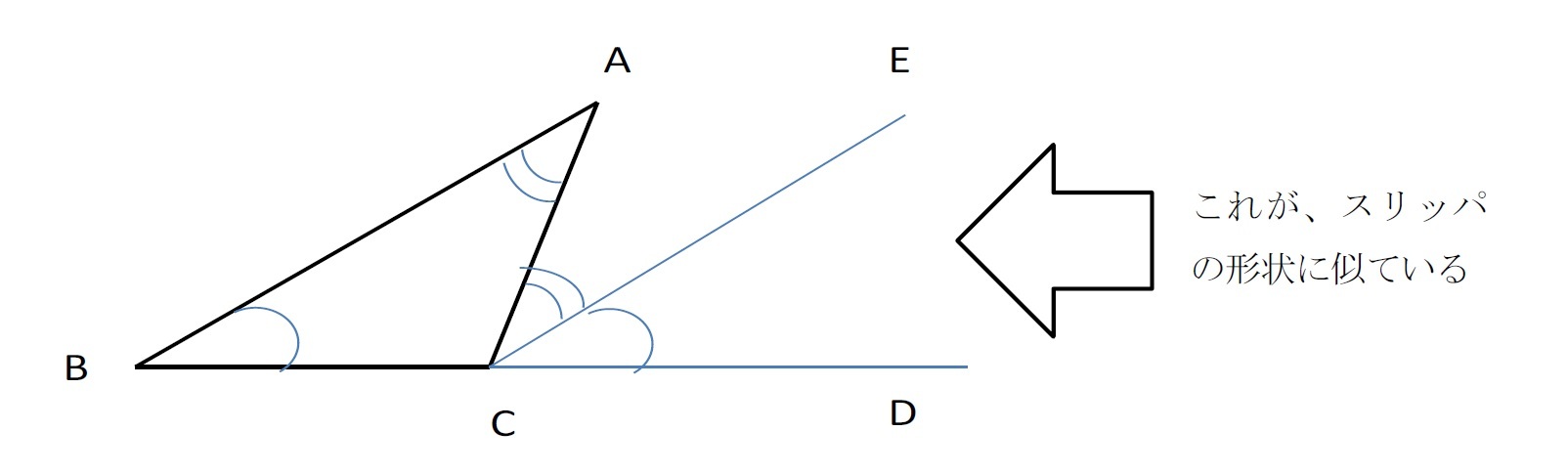


スリッパの法則 って 知っていますか ニッセイ基礎研究所
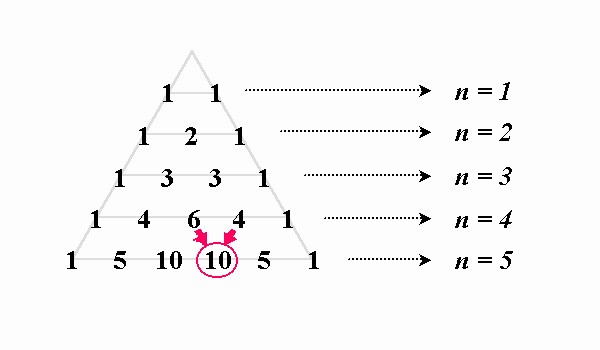


思索の散歩道 パスカルの三角形拡張
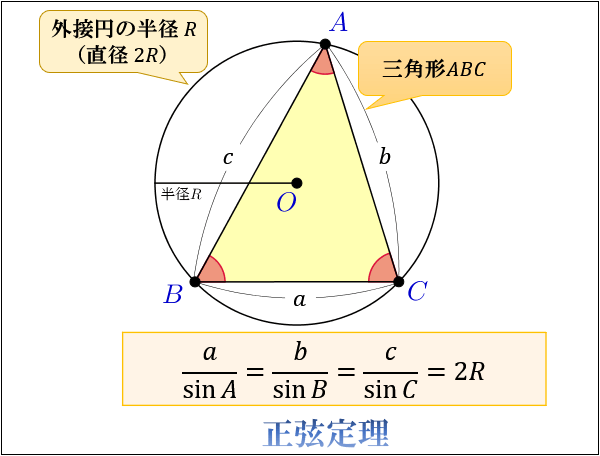


正弦定理とは何か 2つの視点から分かる公式の覚え方 考え方 アタリマエ


チェバの定理 メネラウスの定理
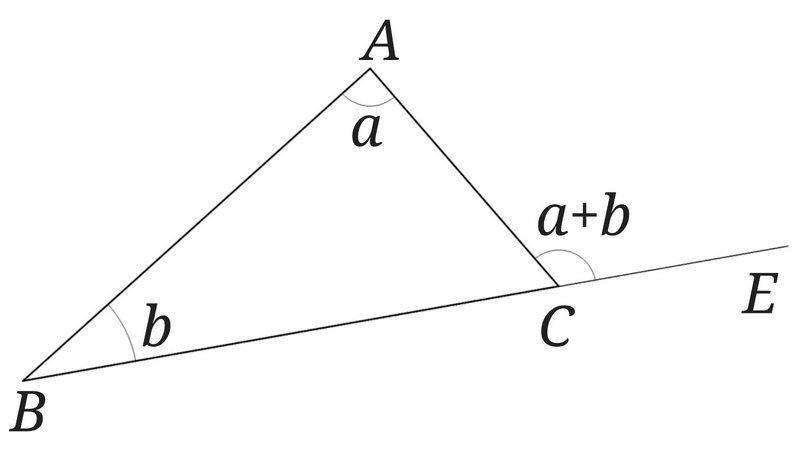


数学の図形で使えるスリッパの法則を使って星の角度の和をだそう まぜこぜ情報局



ヘロンの公式 Wikipedia



三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ



正三角形の高さを求める3つの方法と求め方がわかる3ステップ 言葉 雑学 歴史を知るならmayonez



三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ


中学数学 三角形と比



三角形の内角の和は なぜ180 になるのか スリッパの法則 ブーメランの法則 東大に文理両方で合格した男が綴る 受験の戦略


七五三 三角形から円に内接する四角形へ


3 4 5の三角形で 本当に直角ができる Note Board
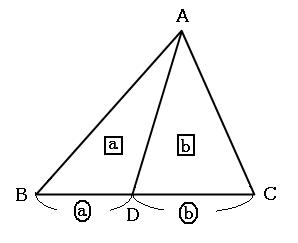


図形の面積と辺の比の関係はテントやドリルで面積を求める



三平方の定理 特別な直角三角形の比を使った計算のやり方は Youtube



三平方の定理と二等辺三角形 Youtube



直角三角形の辺を求める Youtube
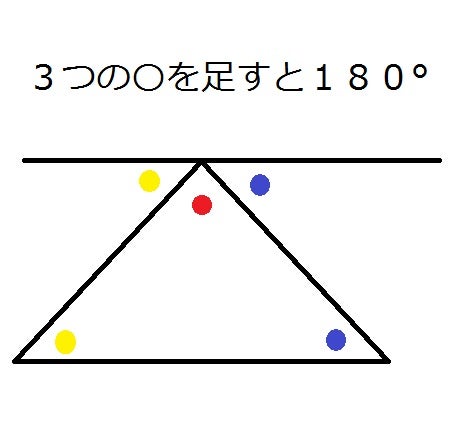


三角形の内角の和は なぜ180 になるのか スリッパの法則 ブーメランの法則 東大に文理両方で合格した男が綴る 受験の戦略
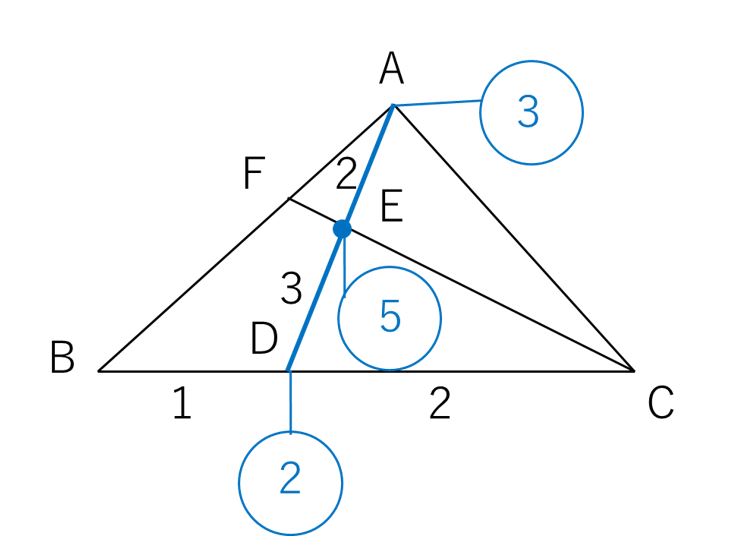


三角形の面積比をてんびんで解く 中学受験プロ講師ブログ



必見 直角二等辺三角形の全てを早稲田生が図で解説 辺の長さや三角比 高校生向け受験応援メディア 受験のミカタ



余弦定理で角度を求める方法 数学の星
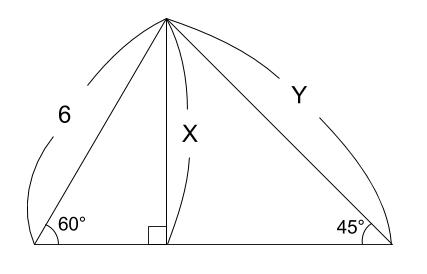


中学数学 三平方の定理 特別な直角三角形 中学数学の無料オンライン学習サイトchu Su



三角形の重心の性質とその証明 求め方 数学a By となりがトトロ マナペディア
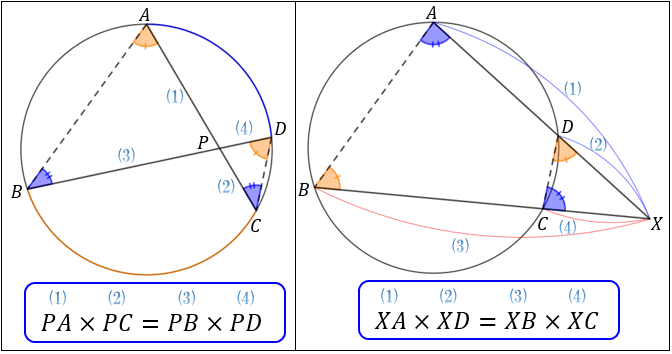


方べきの定理とは 3つのパターンの図解とその証明方法 アタリマエ
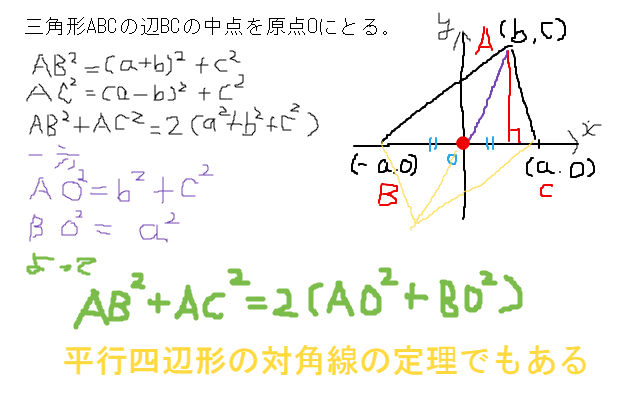


平行四辺形の法則と三角形の中線定理 中学数学 理科 寺子屋塾の復習サイト
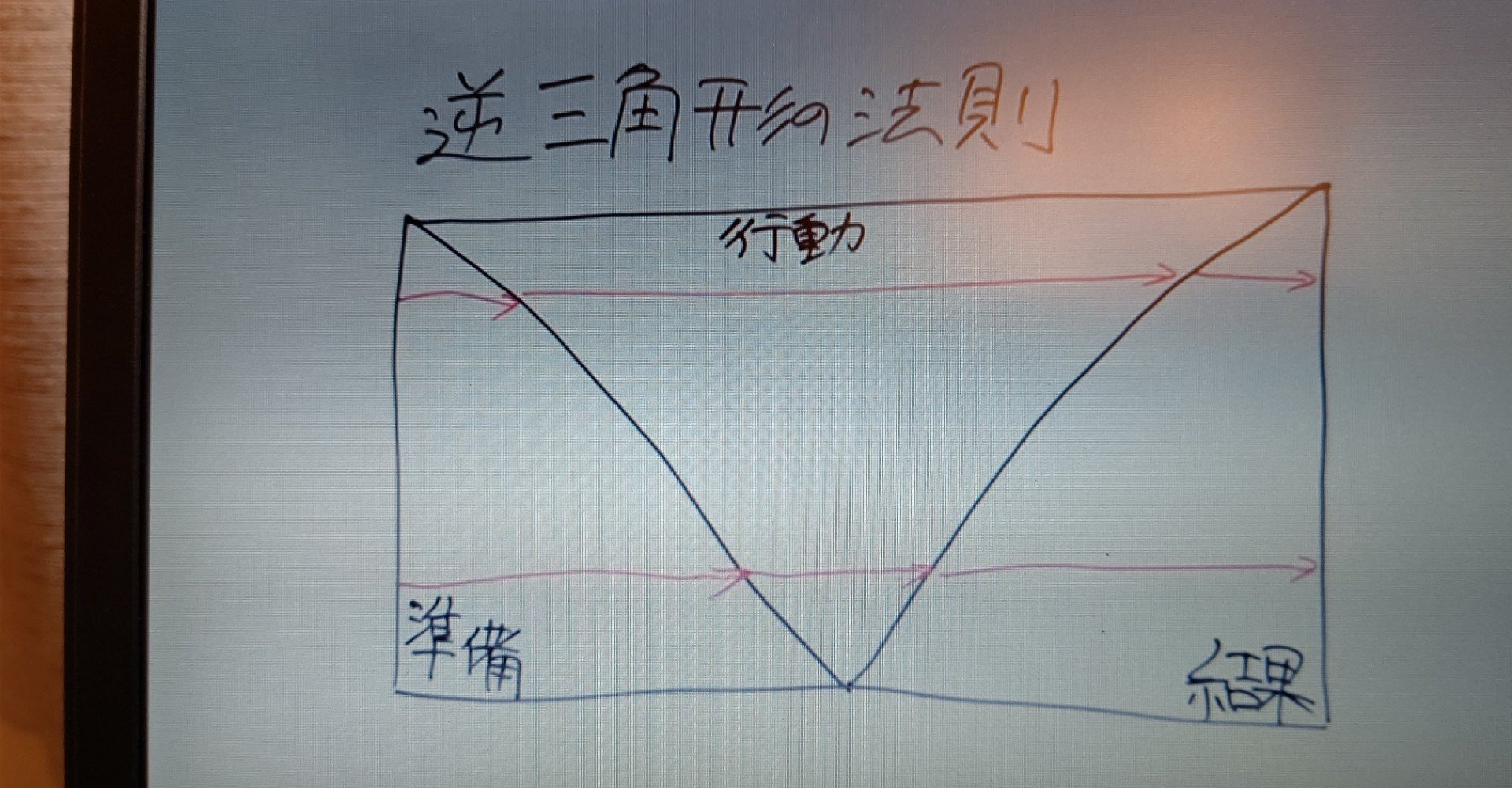


逆三角形の法則とは やすきち2 Note
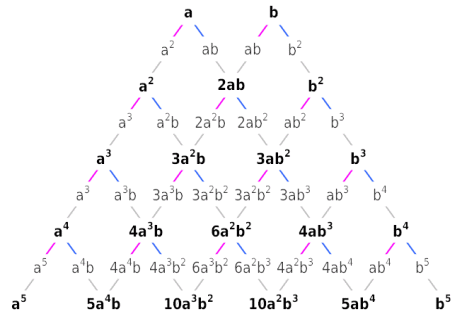


二項定理 パスカルの三角形 大人が学び直す数学



フランク モーリーの定理の証明 高校数学の美しい物語



30 60 90 と 45 45 90 の直角三角形の辺の比 具体例で学ぶ数学



数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



三角形の比 角の二等分線の定理 性質の問題の解き方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



直角三角形の辺の長さ 合同条件 面積について アタリマエ


図形の扉 三角形の外角の定理



正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座 ベネッセコーポレーション
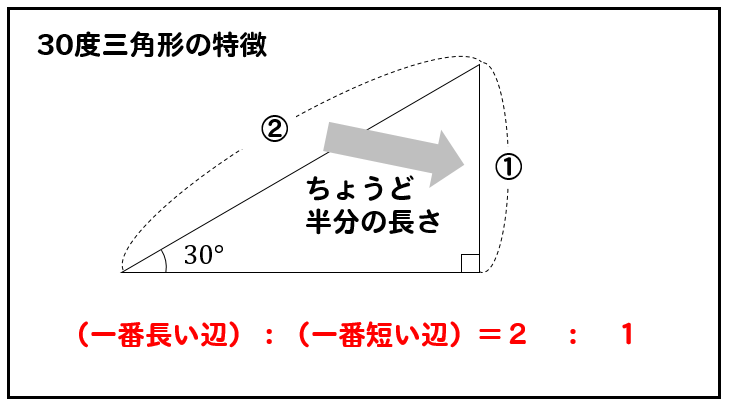


小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ



三平方 ピタゴラス の定理を証明 中学受験算数で出る 直角三角形はコレだ


三角形の面積を2等分する作図 解説 Marupeke Ikd Note



中学数学 中学流 に外接円の半径を求める ジャムと愉快な仲間たち 0名



チェバの定理の証明 覚え方を早稲田生が紹介 問題付き 高校生向け受験応援メディア 受験のミカタ


中学数学 三角形と比



H22年 問17 選択問題 クーロンの法則 3点の点電荷 その他 その他 By Memorandum みんカラ


みんなの算数講座 第86講座 中学受験 家庭教師 東京の算数家庭教師さんじゅつまん



中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット
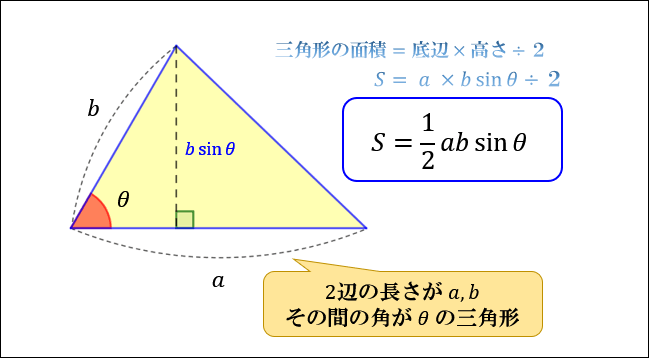


三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ



三平方の定理で辺を求める Youtube



数学 三平方の定理が成り立つ三辺の比 最重要7パターン 受験の秒殺テク 5 勉強の悩み 疑問を解消 小中高生のための勉強サポートサイト Shuei勉強labo



中学3年生 数学 三平方の定理 練習問題プリント ちびむすドリル 中学生



パスカルの三角形と二項定理による展開との関係とは 二項係数の性質を証明 遊ぶ数学



三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ
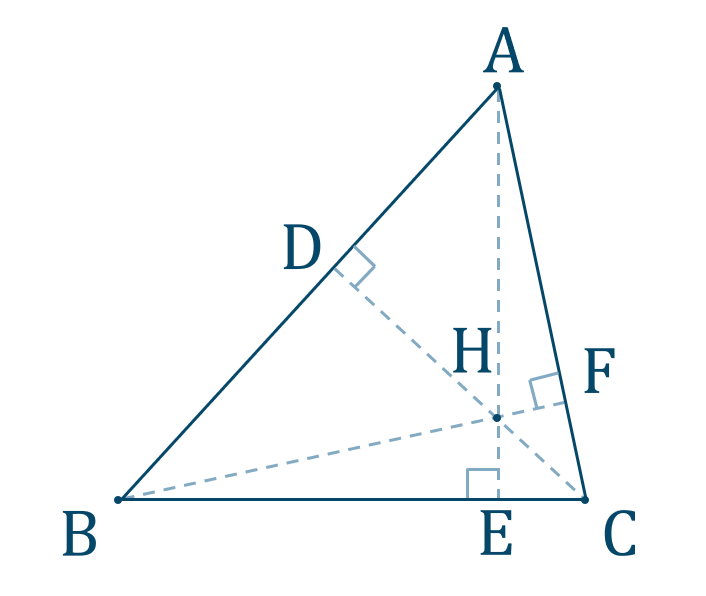


公式一覧と使い方 解き方 数学a 図形の性質 教科書より詳しい高校数学



Excel 三平方の定理で直角三角形の辺の長さ 面積 角度を求める わえなび ワード エクセル問題集
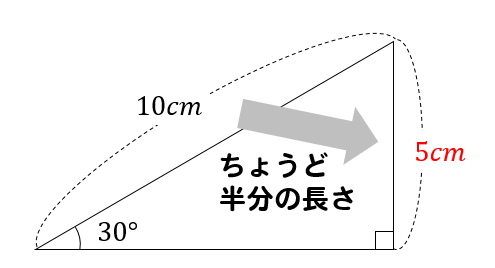


小学算数 30度の三角形ってどうやって面積求める 辺の比は 数スタ



交流回路でよく使う三角形の比 電験三種講座の翔泳社アカデミー



中線定理の3通りの証明 高校数学の美しい物語
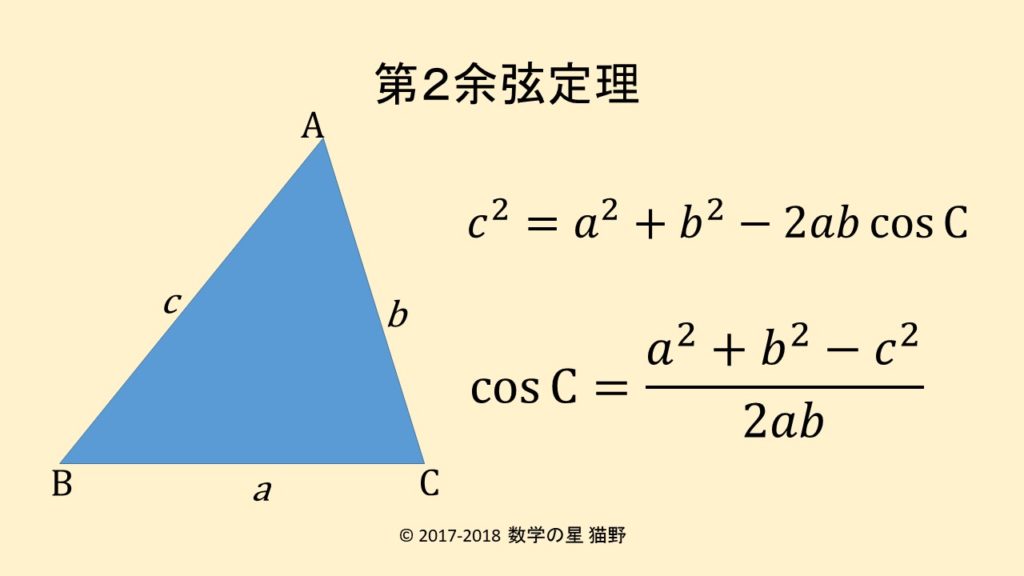


第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星



高校数学a 三角形の内角 外角の二等分線と辺の比の関係とその証明 受験の月



三平方の定理 覚えること 三角定規 苦手な数学を簡単に



中3数学 円周角の定理 の3大重要ポイント 映像授業のtry It トライイット



中3数学 三平方の定理 で最も重要なポイントとは 映像授業のtry It トライイット


